OpenGL "Transformations"
[TRANSFORMATIONS]
1. transformation
- 이전 장까지 사용했던 object는 정적인 object로, 이번 장에서는 각 frame에서 object의 vertex를 수정하고 buffer를 재구성하여 ㅇㅁ직이게 한다
: 이 과정은 번거롭고 processing power를 많이 요구한다
: object를 변환하기 위해 matrix 객체를 사용한다
[Vector]
1. vector
- 가장 기본적 정의로서 vector는 방향이다
: vector는 direction과 magnitude(강도/길이로 알려진 크기)를 가지고 있다
: Ex) 왼쪽으로 10걸음에서, 왼쪽은 vector의 direction이고, 10걸음은 vector에서의 magnitude이다
- 어떠한 차원이든 가질수 있다
: 일반적으로 2~4차원으로 사용한다
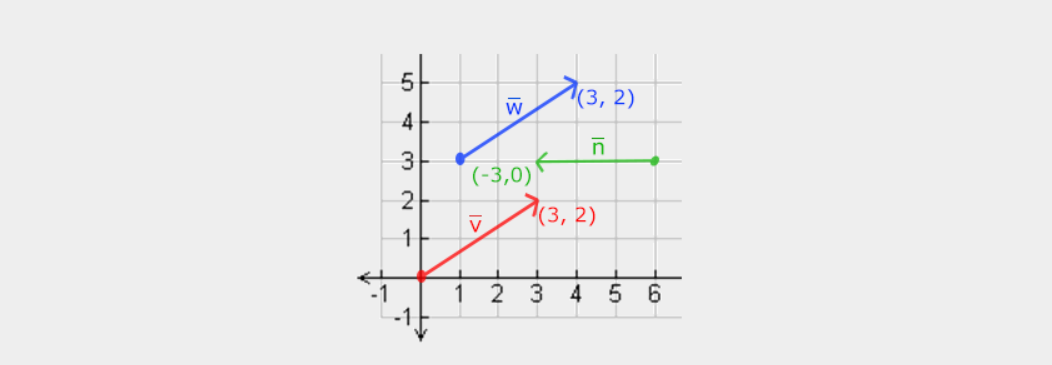
- 위 그림에서 vector는 2D 그래프의 (x, y)를 화살표로 나타낸다
: vector를 2D에서 보여주는 것이 3D에 비해 직관적이므로, 2D vector를 z좌표가 0인 3D vector로 생각할 수 있다
: vector는 방향을 나타내므로 원점의 값은 변경하지 않는다
: v¯ 와 w¯ 는 각 vector의 원점이 다름에도 불구하고 같은 vector이다

- vector는 방향으로서 나타내어지기 떄문에 위치로 표현하기 어려운 경우가 있다
: vector를 위치로 시각화하기 위해서는 direction vector의 원점을 (0, 0, 0)으로 설정한 다음, 점을 지정하는 특정 방향을 가리키면 position vector가 된다
: position vector (3, 5)는 그래프에서 (3, 5)를 가리키고 원점은 (0, 0)이다
: vector 이용하여 2D/3D 공간에서의 방향과 위치를 나타낼 수 있다
: 일반적인 수처럼 vector도 연산을 정의할 수 있다
2. Scalar Vector Operations

- scalar는 하나의 숫자(하나의 요소를 가진 vector)이다
- scalar를 이용해 vector에 대해 사칙연산을 할 때, 간단히 vector의 각 요소들을 scalar로 연산하면 된다
- 위 수식은 각 사칙연산으로 대체하여 사용 가능하나, - 또는 ÷ 의 역순서는 정의되지 않는다
3. Vector Negation

- 역벡터는 vector의 반대 방향을 나타낸다
: 북동쪽을 가리키고 있는 vector의 역벡터는 남서쪽을 가리키는 vector이다
- 이를 만들기 위해서는 vector의 각 요소에 - 기호를 붙이면 된다
: 또는 -1 scalar 곱을 해도 된다
4. Addition and Subtraction

- 두 vector의 덧셈은 component-wise(요소끼리)로서 정의된다
: vector의 각 요소들과 다른 vector의 각 요소들을 더하는 것을 의미한다

- 일반적인 덧셈, 뺄셈과 마찬가지로 vector의 뺄셈은 두 번째 vector의 역벡터를 더한 것과 같다

- 좌측의 그래프는 v = (4, 2)와 k = (1, 2)의 덧셈을 시각화한 그래프다
- 우측의 그래프는 두 vector의 뺄셈을 시각화한 그래프다
: 두 vector를 서로 뺄셈하여 나온 결과는 두 vector가 가리키는 위치의 차이가 된다
5. Length

- vector의 길이/크기를 구하기 위해 Pythagoras theorem(피타고라스 정리)를 사용한다
: vector의 x와 y 요소를 삼각형의 두 변으로 시각화하면 vector가 삼각형을 형성한다

- v의 길이를 알아야하므로 피타고라스 정리를 사용한다
- v¯ vector의 길이는 ||v¯|| 로 표기된다
: 3D에서는 방정식에 z²를 추가함으로써 확장할 수 있다
: 이 사진에서 (4, 2) vector의 길이는 4.47이다

- uniit vector(단위 벡터)는 그 길이가 정확히 1이라는 특성을 가지고 있다
- vector normalizing (벡터 정규화)
: vector의 각 요소들을 길이로 나누면 어떤 vector로부터도 unit vector를 계산할 수 있다
: 오직 방향만을 고려할 때 유용하게 사용한다 (vector의 크기/길이를 변경해도 방향은 변하지 않음)
6. Vector-vector Multiplication
<Dot product_내적>

- 두 vector의 내적은 그 길이의 scalar 곱에 두 vector사이의 각에 cos를 곱한 것과 같다
- 두 벡터 사이의 각은 세타(θ)로 표현된다
: v와 k가 unit vector라면 공식을 단순화할 수 있다
- 내적은 오직 두 vector 사이의 각만을 정의한다
: 각도가 0이면 cos는 1을 나타내고, 각도가 90이면 cos는 0을 나타낸다
: 내적을 이용해 두 vector가 직각인지 아닌지, 혹은 평행하는지 아닌지 확인할 수 있다
: unit vector가 아닌 vector 사이의 각을 계산할 때는 그 결과로부터 두 vector의 길이를 나누어야 cosθ만 남는다

- 내적의 곱셈은 요소들끼리 서로 곱하여 값을 구한다
: 두 unit vector의 내적은 위 그림과 같다 (두 vector의 길이는 1이다)
- 두 vector 사이의 각도를 계산하기 위해 cos⁻¹를 사용한다
: 결과 값은 143.1도이다
- 내적은 빛 계산에 유용하게 사용된다
<Cross product_외적>

- 외적은 오직 3D 공간에서만 정의되고, 평행하지 않는 두 개의 vector를 입력으로 받으며 두 vector에 직교하는 하나의 vector를 만든다
: 입력된 두 vector가 직교한다면 외적의 결과는 3개의 직교 vector가 된다
: 좌측 그림은 외적이 3D공간에서 어떻게 보여지는지 나타낸 그림이다
- 우측 그림은 직교하는 vector A와 vector B를 외적하는 것에 대한 그림이다
: 이 단계를 거치면 입력된 vector와 직교하는 새로운 vector를 얻을 수 있다
[MATRICES]
1. Matrix
- 행렬은 기본적으로 숫자, 기호 수식들의 사각 배열이다
- 행렬은 (i, j)로 인덱싱되며, i는 행이고 j는 열이다
- 2D 그래프를 (x, y)로 인덱싱 할 때와는 정반대로 작용한다
- 행렬은 기본적으로 다진 수학 수식의 사각 배열 그 이상도 이하도 아니다
: 수학적 특성을 가지고 있으며 vector처럼 여러 연산자들을 정의할 수 있다(덧셈, 뺄셈, 곱셈)
2. Addition and Subtraction

- 행렬의 덧셈과 뺄셈은 위 그림과 같이 정의된다
: 두 행렬 사이의 덧셈과 뺄셈은 행렬의 요소별로 수행된다
: 일반적인 수와 동일한 규칙이 적용되지만 동일한 인덱스를 가진 두 행렬의 요소에만 적용된다 (같은 차원의 행렬에서만 적용)
: 3x2 행렬과 2x3행렬은 서로 덧셈과 뺄셈을 수행할 수 없다
3. Matrix-Scalar products

- 행렬-스칼라 곱셈에서는 행렬의 각 요소들을 scalar로 곱한다
- 위 사진의 숫자(scalar)는 기본적으로 행렬의 모든 요소들의 값을 조정(scales)하므로 scalar라고 불린다
4. Matrix-Matrix multiplication
- 행렬 곱셈은 미리 정의된 규칙을 따른다
: 왼쪽 행렬의 열의 개수와 오른쪽 행렬의 행의 개수가 같아야만 곱셈을 수행할 수 있다
: 행렬의 곱셈은 교환법칙이 성립하지 않는다

- 2x2 행렬 곱셈의 계산
: 행과 열의 첫 번째 요소를 시작으로 일반적인 곱셈을 이용하여 결과값을 계산한다
: 결과 행렬은 (왼쪽 행렬의 행 개수, 오른쪽 행렬의 열 개수) 차원으로 나타난다
[MATRIX-VECTOR MULTIPLICATION]
1. Vector
- vector는 기본적으로 Nx1차원의 행렬이다
: N은 vector 요소의 개수다 (N-dimensional vector)
: 행렬과 마찬가지로 숫자들의 배열이지만 오직 하나의 열만을 가지고 있다
- 2D/3D 변환들은 행렬 내부에 있고, vector에 그 행렬을 곱하면 vector가 변환된다
2. Identity Matrix_단위행렬

- OpenGL에서는 일반적으로 4x4 변환 행렬을 가지고 작업한다
: 대부분의 vector 크기가 4이기 때문이다
- 단위행렬은 NxN 행렬이고, 대각선을 제외하고는 0을 갖는 행렬이다
: 가장 간단한 변환 행렬이다
: vector에 아무런 영향을 끼치지 않는다
- 단위 행렬은 일반적으로 다른 변환 행렬을 생성하는 시작점이고, 선형대수학을 더 깊게 파고들었을 때 정리를 증명하고 방정식을 푸는데 매우 유용한 행렬이라는 점에서 변환하지 않는 변환행렬의 의미를 알 수 있다
3. Scaling (크기 조정)
- vector를 scaling할 때, 화살표의 방향은 그대로 둔 채로 원하는만큼 길이를 증가시킨다
: 2, 3차원에서 작업하므로 각각 한 축(x, y or z)을 scaling하는 2, 3개의 scaling 변수의 vector로 scaling을 정의할 수 있다
- v¯ = (3, 2)의 scaling

: x축을 따라 vector를 0.5배로 조정하여 2배로 좁힌다
: y축을 따라 vector를 2배로 조정하여 2배로 확대한다
: 좌측의 그림은 vector 크기를 (0.5, 2)로 조정한 결과인 s¯ vector를 나타낸다
- OpenGL은 일반적으로 3D 공간에서 동작한다
: 2D 공간을 사용할 경우 z의 값을 1로 설정한다
- scale 연산
: scaling 요소가 각 축마다 같지 않으면 non-uniform scale (비균일 조정)이다
: scalar가 모든 축에서 동일하다면 uniform scale(균일 조정)이다

- scale 변수들을 (S1, S2, S3)처럼 나타낸다면 (x, y, z) vector에 대한 scale행렬을 위 그림과 같이 정의할 수 있다
: 3D 공간이므로 4번째 값은 1로 유지한다 (4번째 값인 w 구성요소는 다른 용도로 사용된다)
4. Translation
- Translation은 원본 vector 위에 다른 vector를 더하여 다른 위치의 새로운 vector를 반환하는 작업이다 (vector를 이동)
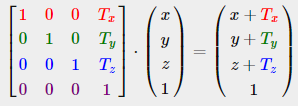
- scaling과 마찬가지로 4x4 행렬에는 특정 작업을 수행하는 데에 사용할 수 있다
: Translation vector를 (Tx, Ty, Tz) 로 표현한다면 옆 그림과 같이 정의할 수 있다
: 모든 변환 값에 vector의 w열을 곱하고 원래의 값에 더하므로 작동한다 (3x3에서는 불가능하다)
< Homogeneous coordinates_동차좌표>
- vector의 w요소는 동차 좌표라고도 불린다
: 동차 좌표로부터 3D vector를 가져오기 위해 x, y, z 좌표를 w 좌표로 나눈다
: 일반적으로 w요소는 1.0이다
- 동차 좌표 생성의 장점
: 3D vector의 이동이 가능하게 한다 (w요소 없이는 vector의 이동이 불가능하다)
+) w 좌표값이 0인 좌표는 이동할 수 없으므로 동차좌표가 0일 경우, vector는 direcction vector라고 불린다
- 이동 행렬을 사용하여 object를 3가지 방향(x, y, z)으로 이동시킬 수 있다
5. Rotation
- 2D, 3D에서의 회전은 각(angle)으로 나타내어진다
: angle은 각도(degree)나 라디안(radian)으로 나타낼 수 있다 (원은 360도와 2PI 라디안으로 나타낼 수 있다)
- 대부분의 회전 함수들은 radian으로 각을 표현한다 (PI = 3.14159265359)
angle in degrees = angle in radians * (180 / PI)
angle in radians = angle in degrees * (PI / 180)
- 반원을 돌리면 180도 회전하고, 1/5을 오른쪽으로 회전하면 72도 회전한다
: vector v¯가 vector k¯에서 오른쪽으로 72도 회전하거나 시계 방향으로 회전하는 기본 2D vector에 대해 입증되었다
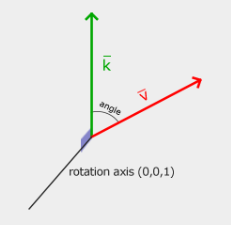
- 3D 회전은 angle과 회전 축으로 지정된다
: 지정된 angle은 주어진 축을 따라 물체를 회전시킨다
: 3D 공간에서 2D vector를 회전시킬 때 회전축을 z축으로 설정한다
- 삼각법을 사용하면 주어진 각도에서 새로 회전하는 vector로 vector를 변환할 수 있다
: 일반적으로 sin 및 cos 조합을 통해 수행된다

- 회전 행렬은 3D 공간에서 각각의 축에 대해 정의된다 (angle은 θ로 나타내어진다)

- 회전 행렬을 사용하면 위치 vector를 세 가지의 축 중 하나에 대해 변환시킬 수 있다
- 임의의 3D 축을 중심으로 회전하려면 먼저 X축을 중심으로 회전한 후, Y, Z축을 차례로 하여 3개를 모두 결합할 수 있다
: 이 방법은 Gimbal lock 문제를 빠르게 발생시키므로, 일반적으로 회전 행렬을 결합하는 방법 대신 임의의 단위 축(0.662, 0.2, 0.722)을 중심으로 즉시 회전한다
: 위 그림은 (Rx, Ry, Rz)를 회전 축으로 하여 행렬을 표현한 것이다
6. Combining Martices
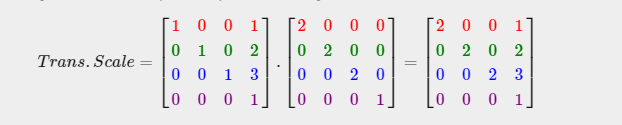
- (x, y, z) vector를 2만큼 scale하고 (1, 2, 3)만큼 이동시키려고 할 때의 결과 변환 행렬이다
: 이동 행렬과 스케일 행렬이 필요하다
- 행렬을 곱할 때에는 먼저 이동을 한 후 scaling을 한다
: 행렬 곱은 교환 법칙이 성립하지 않으므로 순서가 중요하다
: 가장 오른쪽에 있는 행렬이 vector와 처음으로 곱해지므로 곱셈은 오른쪽에서 왼쪽으로 읽어야한다
- 행렬을 조합할 때에는 먼저 scale 연산을 한 후 회전 연산을 하고 마지막에 이동 연산을 한다
: 먼저 이동을 한 후 scaling을 한다면 이동 vector 또한 scale 된다
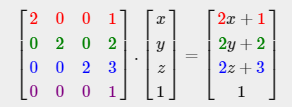
- 변환 행렬을 vector에 적용한 결과이다
- 이 vector는 먼저 2만큼 scale 한 후 (1, 2, 3)만큼 이동한다
[IN PRACTICE]
- OpenGL은 행렬이나 vector 지식에 대한 어떠한 형식도 가지고 있지 않으므로 수학 관련 class와 function을 만들어야한다
: GLM은 OpenGL과 호환되는 수학 라이브러리로, 이를 사용하여 진행한다
1. GLM
- GLM
: OpenGL Mathematics의 약자로, header file 전용 라이브러리이다
: 별도의 Linking이나 Compile이 필요하지 않다
: header file의 root 디렉터리를 include 폴더에 복사하고 시작한다
#include <glm/glm.hpp>
#include <glm/gtc/matrix_transform.hpp>
#include <glm/gtc/type_ptr.hpp>- GLM의 대부분의 기능은 위 코드의 header file에서 찾을 수 있다
glm::vec4 vec(1.0f, 0.0f, 0.0f, 1.0f);
glm::mat4 trans = glm::mat4(1.0f);
trans = glm::translate(trans, glm::vec3(1.0f, 1.0f, 0.0f));
vec = trans * vec;
std::cout << vec.x << vec.y << vec.z << std::endl;- (1, 0, 0) vector를 이동하여 (1, 1, 0) vector로 변환하기 (glm::vec4로 정의하면 1.0으로 설정된 정방행렬이 된다)
: GLM의 vector class를 사용하여 vec vector를 선언한다
: mat4(4x4행렬)를 정의하고 대각선을 1.0으로 초기화하여 행렬을 1D 행렬로 명시적으로 초기화한다 (만약 1D 행렬로 초기화하지 않는다면 행렬은 null행렬이 될 것이고, 이후 모든 행렬 연산도 null 행렬로 끝난다)
: 단위행렬을 transformation행렬과 함께 glm::translate 함수로 전달하여 변환 행렬을 만든다
: 변환 vector와 변환 행렬을 곱한 후 결과를 출력한다 (결과 vector는 (1+1, 0+1, 0+0) 연산을 하여 (2, 1, 0) vector가 된다)
glm::mat4 trans = glm::mat4(1.0f);
trans = glm::rotate(trans, glm::radians(90.0f), glm::vec3(0.0, 0.0, 1.0));
trans = glm::scale(trans, glm::vec3(0.5, 0.5, 0.5));- container object의 크기를 조정하고 회전하기
: container를 각 축에 대해 0.5만큼 scale하고 Z축을 중심으로 90도 회전시킨다
: GLM은 각을 radian으로 받아오므로 glm::radians function을 사용하여 각도를 radian으로 변환시킨다
- rotate = (0.0, 0.0, 1.0) : z축을 기준으로 회전
: 이러한 texture가 입혀진 사각형은 XY 평면이기 때문에 Z축을 중심으로 회전하려고 한다 (회전 축은 단위 벡터여야하므로, X, Y 또는 Z축을 중심으로 회전하지 않을 경우에는 vector가 정규화 되었는지 확인한다)
- scale = (0.5, 0.5, 0.5) : 균등 크기 조절, 2배 작게 조정한다
GLM의 각 함수에 행렬을 전달하기 때문에 GLM은 행렬을 자동으로 곱하고 모든 변환이 조합된 변환행렬을 return한다
#version 330 core
layout (location = 0) in vec3 aPos;
layout (location = 1) in vec2 aTexCoord;
out vec2 TexCoord;
uniform mat4 transform;
void main()
{
gl_Position = transform * vec4(aPos, 1.0f);
TexCoord = vec2(aTexCoord.x, aTexCoord.y);
}- shader에서 변환행렬을 가져오는 방법
: mat4 uniform 변수를 받아들일 수 있도록 vertex shader를 적용하고, 위치 vector에 행렬 uniform을 곱한다
- GLSL에는 vector와 swizzling과 같은 연산을 가능하게 하는 mat2와 mat3 type도 있다
: 모든 수학 연산(scalar*matrix, matrix*vector, matrix*matrix 등)은 행렬 type위에서 가능하다
unsigned int transformLoc = glGetUniformLocation(ourShader.ID, "transform");
glUniformMatrix4fv(transformLoc, 1, GL_FALSE, glm::value_ptr(trans));- uniform 설정
: gl_Position에 전달하기 전에 변환 행렬과 위치 vector를 곱해주었다
: container가 2배로 작고 90도 회전(왼쪽으로) 해야하므로 변환 행렬을 shader에 전달해야한다
- glUniformMatrix4fv(location, matrix의 개수, column-major ordering, 실제 행렬 데이터)
: 행렬 데이터를 shader에 보낸다
: column-major ordering은 GLM의 기본 행렬 layout인 내부행렬 layout을 사용한다 (행과 열을 바꿀 필요가 없으면 false로 지정한다)
: 실제 행렬 데이터는 value_ptr function을 사용하여 행렬을 변환해 type을 맞춘다
+) reinterpret_cast<float*>(&trans) == glm::value_ptr(trans) == &trans[0][0]
: reinterpret_cast는 모든 pointer type 간의 형 변환을 허용한다 (static_cast는 오직 상속 관계의 pointer끼리만, compile 시간에 캐스팅 완료)
: 이전 값에 대한 바이너리를 유지 (type에 따라 출력되는 값이 다를 수 ㅇ있음)
2. Result

3. GLM_Additionally
glm::mat4 trans = glm::mat4(1.0f);
trans = glm::translate(trans, glm::vec3(0.5f, -0.5f, 0.0f));
trans = glm::rotate(trans, (float)glfwGetTime(), glm::vec3(0.0f, 0.0f, 1.0f));- 시간에 따라 계속 회전하고 container를 window의 우측 하단으로 위치시키기
: loop안에서 변환 행렬을 계속 수정해야한다
: 시간에 따른 각을 얻기 위해 GLFW의 시간 함수를 사용한다
: 일반적으로 화면을 render할 때 loop가 돌 때마다 새로운 값으로 재생성된 여러 변환 해렬들을 사용합니다
- container를 (0, 0, 0)을 중심으로 회전시키고 회전된 container를 화면 우측 하단으로 이동시킨다
: code에서는 이동 후에 회전을 시켰지만, 실제 변환 순서는 거꾸로 진행된다
+) vertex shader에서 변환을 사용하면 데이터를 계속해서 다시 전달할 필요가 없기 때문에 vertex 데이터를 다시 정의하는 수고를 덜어주고 작업 시간을 아낄 수 있다
[CODE]
#include <glad/glad.h>
#include <GLFW/glfw3.h>
#define STB_IMAGE_IMPLEMENTATION
#include <stb_image.h>
#include <glm/glm.hpp>
#include <glm/gtc/matrix_transform.hpp>
#include <glm/gtc/type_ptr.hpp>
#include <learnopengl/shader_s.h>
#include <iostream>
void framebuffer_size_callback(GLFWwindow* window, int width, int height);
void processInput(GLFWwindow* window);
// settings
const unsigned int SCR_WIDTH = 800;
const unsigned int SCR_HEIGHT = 600;
int main()
{
// glfw: initialize and configure
// ------------------------------
glfwInit();
glfwWindowHint(GLFW_CONTEXT_VERSION_MAJOR, 3);
glfwWindowHint(GLFW_CONTEXT_VERSION_MINOR, 3);
glfwWindowHint(GLFW_OPENGL_PROFILE, GLFW_OPENGL_CORE_PROFILE);
#ifdef __APPLE__
glfwWindowHint(GLFW_OPENGL_FORWARD_COMPAT, GL_TRUE);
#endif
// glfw window creation
// --------------------
GLFWwindow* window = glfwCreateWindow(SCR_WIDTH, SCR_HEIGHT, "LearnOpenGL", NULL, NULL);
if (window == NULL)
{
std::cout << "Failed to create GLFW window" << std::endl;
glfwTerminate();
return -1;
}
glfwMakeContextCurrent(window);
glfwSetFramebufferSizeCallback(window, framebuffer_size_callback);
// glad: load all OpenGL function pointers
// ---------------------------------------
if (!gladLoadGLLoader((GLADloadproc)glfwGetProcAddress))
{
std::cout << "Failed to initialize GLAD" << std::endl;
return -1;
}
// build and compile our shader zprogram
// ------------------------------------
Shader ourShader("5.1.transform.vs", "5.1.transform.fs");
// set up vertex data (and buffer(s)) and configure vertex attributes
// ------------------------------------------------------------------
float vertices[] = {
// positions // texture coords
0.5f, 0.5f, 0.0f, 1.0f, 1.0f, // top right
0.5f, -0.5f, 0.0f, 1.0f, 0.0f, // bottom right
-0.5f, -0.5f, 0.0f, 0.0f, 0.0f, // bottom left
-0.5f, 0.5f, 0.0f, 0.0f, 1.0f // top left
};
unsigned int indices[] = {
0, 1, 3, // first triangle
1, 2, 3 // second triangle
};
unsigned int VBO, VAO, EBO;
glGenVertexArrays(1, &VAO);
glGenBuffers(1, &VBO);
glGenBuffers(1, &EBO);
glBindVertexArray(VAO);
glBindBuffer(GL_ARRAY_BUFFER, VBO);
glBufferData(GL_ARRAY_BUFFER, sizeof(vertices), vertices, GL_STATIC_DRAW);
glBindBuffer(GL_ELEMENT_ARRAY_BUFFER, EBO);
glBufferData(GL_ELEMENT_ARRAY_BUFFER, sizeof(indices), indices, GL_STATIC_DRAW);
// position attribute
glVertexAttribPointer(0, 3, GL_FLOAT, GL_FALSE, 5 * sizeof(float), (void*)0);
glEnableVertexAttribArray(0);
// texture coord attribute
glVertexAttribPointer(1, 2, GL_FLOAT, GL_FALSE, 5 * sizeof(float), (void*)(3 * sizeof(float)));
glEnableVertexAttribArray(1);
// load and create a texture
// -------------------------
unsigned int texture1, texture2;
// texture 1
// ---------
glGenTextures(1, &texture1);
glBindTexture(GL_TEXTURE_2D, texture1);
// set the texture wrapping parameters
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_S, GL_REPEAT);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_T, GL_REPEAT);
// set texture filtering parameters
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_LINEAR);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_LINEAR);
// load image, create texture and generate mipmaps
int width, height, nrChannels;
stbi_set_flip_vertically_on_load(true); // tell stb_image.h to flip loaded texture's on the y-axis.
unsigned char* data = stbi_load("container.jpg", &width, &height, &nrChannels, 0);
if (data)
{
glTexImage2D(GL_TEXTURE_2D, 0, GL_RGB, width, height, 0, GL_RGB, GL_UNSIGNED_BYTE, data);
glGenerateMipmap(GL_TEXTURE_2D);
}
else
{
std::cout << "Failed to load texture" << std::endl;
}
stbi_image_free(data);
// texture 2
// ---------
glGenTextures(1, &texture2);
glBindTexture(GL_TEXTURE_2D, texture2);
// set the texture wrapping parameters
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_S, GL_REPEAT);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_T, GL_REPEAT);
// set texture filtering parameters
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_LINEAR);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_LINEAR);
// load image, create texture and generate mipmaps
data = stbi_load("awesomeface.png", &width, &height, &nrChannels, 0);
if (data)
{
// note that the awesomeface.png has transparency and thus an alpha channel, so make sure to tell OpenGL the data type is of GL_RGBA
glTexImage2D(GL_TEXTURE_2D, 0, GL_RGB, width, height, 0, GL_RGBA, GL_UNSIGNED_BYTE, data);
glGenerateMipmap(GL_TEXTURE_2D);
}
else
{
std::cout << "Failed to load texture" << std::endl;
}
stbi_image_free(data);
// tell opengl for each sampler to which texture unit it belongs to (only has to be done once)
// -------------------------------------------------------------------------------------------
ourShader.use();
ourShader.setInt("texture1", 0);
ourShader.setInt("texture2", 1);
// render loop
// -----------
while (!glfwWindowShouldClose(window))
{
// input
// -----
processInput(window);
// render
// ------
glClearColor(0.46667f, 0.533333f, 0.6f, 1.0f);
glClear(GL_COLOR_BUFFER_BIT);
// bind textures on corresponding texture units
glActiveTexture(GL_TEXTURE0);
glBindTexture(GL_TEXTURE_2D, texture1);
glActiveTexture(GL_TEXTURE1);
glBindTexture(GL_TEXTURE_2D, texture2);
// create transformations
glm::mat4 transform = glm::mat4(1.0f); // make sure to initialize matrix to identity matrix first
transform = glm::translate(transform, glm::vec3(0.5f, -0.5f, 0.0f));
transform = glm::rotate(transform, (float)glfwGetTime(), glm::vec3(0.0f, 0.0f, 1.0f));
// get matrix's uniform location and set matrix
ourShader.use();
unsigned int transformLoc = glGetUniformLocation(ourShader.ID, "transform");
glUniformMatrix4fv(transformLoc, 1, GL_FALSE, glm::value_ptr(transform));
// render container
glBindVertexArray(VAO);
glDrawElements(GL_TRIANGLES, 6, GL_UNSIGNED_INT, 0);
// glfw: swap buffers and poll IO events (keys pressed/released, mouse moved etc.)
// -------------------------------------------------------------------------------
glfwSwapBuffers(window);
glfwPollEvents();
}
// optional: de-allocate all resources once they've outlived their purpose:
// ------------------------------------------------------------------------
glDeleteVertexArrays(1, &VAO);
glDeleteBuffers(1, &VBO);
glDeleteBuffers(1, &EBO);
// glfw: terminate, clearing all previously allocated GLFW resources.
// ------------------------------------------------------------------
glfwTerminate();
return 0;
}
// process all input: query GLFW whether relevant keys are pressed/released this frame and react accordingly
// ---------------------------------------------------------------------------------------------------------
void processInput(GLFWwindow* window)
{
if (glfwGetKey(window, GLFW_KEY_ESCAPE) == GLFW_PRESS)
glfwSetWindowShouldClose(window, true);
}
// glfw: whenever the window size changed (by OS or user resize) this callback function executes
// ---------------------------------------------------------------------------------------------
void framebuffer_size_callback(GLFWwindow* window, int width, int height)
{
// make sure the viewport matches the new window dimensions; note that width and
// height will be significantly larger than specified on retina displays.
glViewport(0, 0, width, height);
}